점 모으기
문제
행의 크기와 열의 크기가 각각 N인 격자공간에 M개의 점이 있다. N=4이고 M=4인 경우의 예가 아래에 있다.
격자공간 왼쪽의 숫자는 행 번호이며, 위의 숫자는 열 번호를 나타낸다.
그리고 격자공간내의 각 사각형의 위치는 (행 번호, 열 번호)로 표시한다.
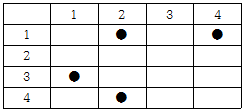
이제 격자공간에 있는 모든 점들을 하나의 사각형안으로 모으려고 한다.
어떤 점을 움직일 때는 그 점이 들어있는 사각형에서 상하좌우로 인접한 사각형으로만 움직일 수 있다.
여기에서는 격자공간내의 한 사각형으로 모든 점들을 모을 때 각 점이 움직인 거리의 합을 고려한다.
예를 들어, 위의 점들을 (3,2)에 있는 사각형으로 모을 때 최단거리로 점들을 이동시킨다면 (1,2)에 있는 점의 이동거리는 2이고,
(3,1)과 (4,2)에 있는 점의 이동거리는 각각 1이며, (1,4) 에 있는 점의 이동거리는 4이므로 점들이 움직인거리의 합은 8이다.
또, 위의 모든 점들을 (1,2)의 위치로 모을 때도 점들이 이동한 거리의 합이 8 임을 알 수 있다.
위의 예에서는 점들을 어떤 하나의 사각형으로 모을 때 이동거리의 합이 8보다 작게 되는 사각형은 없다.
이 문제는 주어진 격자공간에 있는 모든 점들을 하나의 사각형으로 모을 때 드는 이동거리의 합의 최솟값을 구하는 것이다.
주어진 격자공간에서는 하나의 사각형에 여러 개의 점들이 들어 있을 수도 있고,
점들을 모을 때는 어떤 점이 들어 있는 사각형으로도 모을 수 있다고 가정한다.
입력형식
첫 줄에는 격자공간의 크기와 점들의 개수를 나타내는 두 정수 N과 M이 하나의 공백을 사이에 두고 주어진다.
다음의 M줄에는 각 줄마다 격자공간내의 점의 위치를 나타내는 두 개의 정수가 하나의 공백을 사이에 두고 주어진다.
단, N의 크기는 1이상 10,000이하이고, M의 크기는 1이상 100,000이하이다.
출력형식
입력 예
4 4
1 2
1 4
3 1
4 2
출력 예
8
소스코드
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define M 100100
int n, m, x[M], y[M], X, Y, s;
int compare(const void* a, const void* b)
{
if (*(int*)a > * (int*)b)
return 1;
else if (*(int*)a < *(int*)b)
return -1;
else
return 0;
}
int main()
{
int i;
scanf("%d %d", &n, &m);
for (i = 0; i < m; i++)
scanf("%d %d", &x[i], &y[i]);
qsort(x, m, sizeof(x[0]), compare);
qsort(y, m, sizeof(y[0]), compare);
X = x[m / 2];
Y = y[m / 2];
s = 0;
for (i = 0; i < m / 2; i++)
s += (X - x[i]) + (Y - y[i]);
for (; i < m; i++)
s += (x[i] - X) + (y[i] - Y);
printf("%d\n", s);
return 0;
}

